Principles of NMR
By John C. Edwards, Ph.D.
Principles of NMR pdf
Nuclear magnetic resonance spectroscopy (NMR) was first developed in 1946 by research groups at Stanford and M.I.T., in the USA. The radar technology developed during World War II made many of the electronic aspects of the NMR spectrometer possible. With the newly developed hardware physicists and chemists began to apply the technology to chemistry and physics problems. Over the next 50 years NMR developed into the premier organic spectroscopy available to chemists to determine the detailed chemical structure of the chemicals they were synthesizing. Another well-known product of NMR technology has been the Magnetic Resonance Imager (MRI), which is utilized extensively in the medical radiology field to obtain image slices of soft tissues in the human body. In recent years, NMR has moved out of the research laboratory and into the on-line process analyzer market. This has been made possible by the production of stable permanent magnet technologies that allow high-resolution 1H NMR spectra to be obtained in a process environment.
The NMR phenomenon is based on the fact that nuclei of atoms have magnetic properties that can be utilized to yield chemical information. Quantum mechanically subatomic particles (electrons, protons and neutrons) can be imagined as spinning on their axes. In many atoms (such as 12C) these spins are paired against each other, such that the nucleus of the atom has no overall spin. However, in many atoms (such as 1H and 13C) the nucleus does possess an overall spin. The rules for determining the net spin of a nucleus are as follows:
- If the number of neutrons and the number of protons are both even, then the nucleus has NO spin.
- If the number of neutrons plus the number of protons is odd, then the nucleus has a half-integer spin (i.e. 1/2, 3/2, 5/2)
- If the number of neutrons and the number of protons are both odd, then the nucleus has an integer spin (i.e. 1, 2, 3)
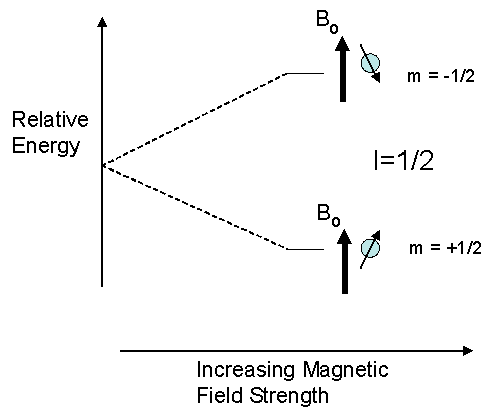
The overall spin, I, is important. Quantum mechanics tells us that a nucleus of spin I will have 2I + 1 possible orientations. A nucleus with spin 1/2 will have 2 possible orientations. In the absence of an external magnetic field, these orientations are of equal energy. If a magnetic field is applied, then the energy levels split. Each level is given a magnetic quantum number, m.
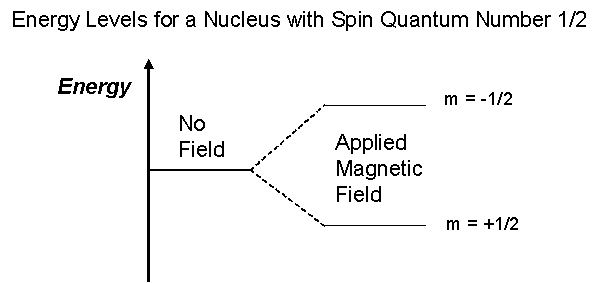
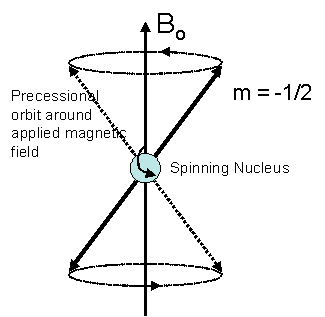
In quantum mechanical terms, the nuclear magnetic moment of a nucleus can align with an externally applied magnetic field of strength Bo in only 2I+1 ways, either with or against the applied field Bo. For a single nucleus with I=1/2 and positive g, only one transition is possible (D I=1, a single quantum transition) between the two energy levels The energetically preferred orientation has the magnetic moment aligned parallel with the applied field (spin m=+1/2) and is often given the notation a, whereas the higher energy anti-parallel orientation (spin m=-1/2) is referred to as b. The rotational axis of the spinning nucleus cannot be orientated exactly parallel (or anti-parallel) with the direction of the applied field Bo (defined in our coordinate system as about the z axis) but must precess (motion similar to a gyroscope) about this field at an angle, with an angular velocity given by the expression:
wo = gBo
Where wo is the precession rate called the Larmor frequency. The constant g is called the magnetogyric ratio and relates the magnetic moment m and the spin number I for any specific nucleus:
g = 2pm/hI
Each nucleus has a characteristic value of g, which is defined as a constant of proportionality between the nuclear angular momentum and magnetic moment. For a proton, g = 2.674×104 gauss-1 sec-1. This precession process generates an electric field with frequency wo. If we irradiate the sample with radio waves (MHz) the proton can absorb the energy and be promoted to the less favorable higher energy state. This absorption is called resonance because the frequency of the applied radiation and the precession coincide or resonate.
We can calculate the resonance frequencies for different applied field (Bo) strengths (in Gauss):
| Bo | MHz |
| 14100 | 60 |
| 23500 | 100 |
| 47000 | 200 |
| 70500 | 300 |
| 94000 | 400 |
| 117500 | 500 |
The field strength of a magnet is usually reported at the resonance frequency for a proton. Therefore, for different nuclei with different gyromagnetic ratios, different frequencies must be applied in order to achieve resonance.
NMR Energies
The orientations a magnetic nucleus can take against an external magnetic are not of equal energy. Spin states which are oriented parallel to the external field are lower in energy than in the absence of an external field. In contrast, spin states whose orientations oppose the external field are higher in energy than in the absence of an external field.
Where an energy separation exists there is a possibility to induce a transition between the various spin states. By irradiating the nucleus with electromagnetic radiation of the correct energy (as determined by its frequency), a nucleus with a low energy orientation can be induced to “jump” to a higher energy orientation. The absorption of energy during this transition forms the basis of the NMR method. Other spectroscopic methods, such as IR and UV/Visible, also rely on the absorption of energy during a transition although the nature and energies of the transitions vary widely.
When discussing NMR you will find that spin state energy separations are often characterized by the frequency required to induce a transition between the states. While frequency is not a measure of energy, the simple relationship E=hυ (where E=energy, h=Planks constant, and υ=frequency) makes this substitution understandable. The statement “the transition (peak) shifted to higher frequencies” should be read as “the energy separation increased”.
Comparison of various spectroscopic methods
| NMR | ~60×106 to 600×106 Hz | Probes nucleus’ magnetic field |
| ESR | ~1×109 to 30×109 Hz | Probes electron’s magnetic field |
| Microwave | ~1×109 to 600×109 Hz | Probes molecular rotation |
| Infrared | ~6×1011 to 4000×1011 Hz | Probes bond vibrations and bending |
| Ultraviolet/Visible | ~7.5×1014 to 300×1014 Hz | Probes outer core electron transitions |
Population Distribution
In a given sample of a specific NMR-active nucleus, the nuclei will be distributed throughout the various spin states available. As the energy separation between these states is comparatively small, energy from thermal collisions is sufficient to place many nuclei into higher energy spin states. The number of nuclei in each spin state is described by the Boltzmann distribution :
Nupper /Nlower = e-γBo/kT
where the N values are the numbers of nuclei in the respective spin states, γ is the magnetogyric ratio, h is Planck’s constant, Bo is the external magnetic field strength, k is the Boltzmann constant, and T is the temperature. For example, given a sample of 1H nuclei in an external magnetic field of 1.41 Tesla
Population Ratio = e((-2.67519×108 rad.s-1.T-1*1.41T*6.626176×10-34 J.s)/(1.380662×10-23 J.K-1*K 293)) = 0.9999382
At room temperature, the ratio of the upper to lower energy populations is 0.9999382. In other words, the upper and lower energy spin states are almost equally populated with only a very small excess in the lower energy state. (In reality, this means that the population difference is only about 123 for every 4,000,000 spins).
This nearly equal population distribution has a very important consequence. The signal intensity of any spectroscopic method depends largely on the population difference between the two energy levels involved. When a system is irradiated with a frequency, whose energy matches that separating the levels, transitions will be induced not only from the lower energy level to the higher, but also in the reverse direction. Upward transitions absorb energy while downward transitions release energy. The number of transitions in either direction is given by multiplying the starting level population by a probability. This probability is the same for transitions in either direction. If the energy level populations are the same, the number of transitions in either direction will also be the same. The absorption and release of energy will balance each other to zero and there will be nothing to observe. Only when the populations are not equal is there a net absorption or release of energy to observe.
Energy levels in a spectroscopic technique such as UV/Visible spectroscopy are far apart in energy and, according to the Boltzmann distribution, the population resides almost entirely in the lowest energy state. As a result, UV/Visible spectroscopy is an extremely sensitive technique and is commonly used in analytical chemistry to deal with very small amounts of sample. In NMR, the energy separation of the spin states is comparatively very small and while NMR is very informative, quantum mechanically it is considered to be an insensitive technique.
NMR Instrumentation – General Overview
There are two general types of NMR instrument; continuous wave and Fourier transform. Early experiments were conducted with continuous wave (C.W.) instruments, and in 1970 the first Fourier transform (F.T.) instruments became available. This type now dominates the market.
Continuous Wave (CW) NMR instruments
Continuous wave NMR spectrometers are similar in principle to optical spectrometers. The sample is held in a strong magnetic field, and the frequency of the source is slowly scanned (in some instruments, the source frequency is held constant, and the field is scanned).
Fourier Transform (FT) NMR instruments
The magnitude of the energy changes involved in NMR spectroscopy is very small. This means that, sensitivity can be a limitation when looking at very low concentrations. One way to increase sensitivity would be to record many spectra, and then add them together. As noise is random, it adds as the square root of the number of spectra recorded. For example, if one hundred spectra of a compound were recorded and summed, then the noise would increase by a factor of ten, but the signal would increase in magnitude by a factor of one hundred – giving a large increase in sensitivity. However, if this is done using a continuous wave instrument, the time needed to collect the spectra is very large (one scan takes two to eight minutes).
In FT-NMR, all frequencies in a spectrum are irradiated simultaneously with a radio frequency pulse. A single oscillator (transmitter) is used to generate a pulse of electromagnetic radiation of frequency w but with the pulse truncated after only a few complete cycles (corresponding to a duration τ) so that the waveform has rectangular as well as sinusoidal characteristics. It can be proven that the frequencies contained within this pulse are within the range +/- 1/τ of the main frequency wo. For example a 5 μs pulse would generate a range of frequencies of wo ± 1/0.000005 Hz (i.e. wo ± 200,000 Hz).
Following the pulse, the nuclei return to thermal equilibrium. A time domain emission signal (called a free induction decay (FID)) is recorded by the instrument as the nuclei relax back to equilibrium. A frequency domain spectrum is then obtained by Fourier transformation of the FID.
The pulse
If a signal of frequency, ƒ, is turned on and then off again very rapidly, then the result is an output consisting of many frequencies centered about ƒ with a bandwidth of 1/τ, where τ is the duration of the pulse. This means that radiation is produced of all frequencies in the range ƒ ± 1/τ. If τ is very small, then a large range of frequencies will be produced simultaneously, and all target nuclei in a sample will be excited.
The effect of applying the pulse
To understand the effect of the radio frequency pulse, consider the precessing magnetic moments of the 1H nuclei:
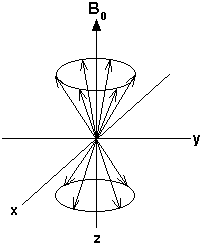
As discussed previously, there are more magnetic moments aligned with the field than against it. This means that when all the opposing magnetic moments have cancelled each other out, the net population difference will create a bulk magnetization vector (called Mo) aligned along the direction of Bo. With this bulk magnetization vector idea the magnetic behavior of the system can be shown like this:
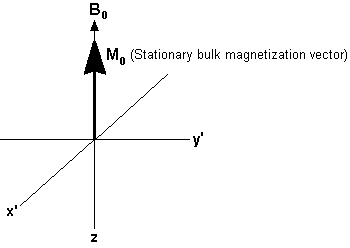
Now we come to the “resonance” aspect of the NMR technique. One has now reduced the magnetic moment system to a bulk magnetization vector. However, one must now take into account the fact that the individual magnetization vectors for the nuclei are still precessing around the applied field at the Larmor frequency (58 MHz in the case of the Foxboro NMR system). The trick in the NMR experiment is to find a way to perturb these magnetic moments away from their alignment with the huge applied field by utilizing the tiny field applied by a radio frequency pulse. This is a problem similar to what one would face when trying to push a friend off a carousel horse with your little finger while the carousel rapidly spins past you at 58 million revolutions per second. Timing would be essential! The way to do this is to jump on the carousel and poke your friend in the eye causing them to fall off the horse. This “jumping on the carousel” can be described as you joining your friends “rotating frame of reference”, in which the friend is static with respect to the observer and can then be acted upon. In the NMR experiment one applies radio frequency pulses at the Larmor frequency of the 1H nuclei being observed in order to perturb the 1H magnetic moments with the magnetic component of the applied RF electromagnetic radiation. In our diagrams below, a short RF pulse is applied along the x’ axis. The magnetic field of this radiation is given the symbol B1. In the rotating frame of reference, B1 and M0 are stationary, and at right angles. The pulse causes the bulk magnetization vector, M0 , to rotate clockwise about the x’ axis. The extent of the rotation is determined by the duration of the pulse. In many FT-NMR experiments, the duration of the pulse is chosen so that the magnetization vector rotates by 90°. In the case of the Foxboro NMR product the duration of the pulse is chosen so that the magnetization vector moves through a 45o rotation.

(The various reasons for performing 45o pulses rather than 90o pulses are related to the relaxation rates of the spins. After each pulse one must wait for a “relaxation period” which allows time for all the spins to equilibrate and line up with Bo again. By performing a 45o pulse one can collect the NMR spectra at 3 times the rate that is possible after performing a 90o pulse, while still acquiring 70% of the signal).
The detector is aligned along the y’-axis. If we return to a static frame of reference (i.e. stop spinning the laboratory at the Larmor frequency) the net magnetic moment will be spinning around the y-axis at the Larmor frequency. This motion constitutes a radio-frequency signal, which can be detected. When the pulse ends, the nuclei relax and return to their equilibrium positions, and the signal decays. This decaying signal contains the sum of the frequencies from all the target nuclei. It is picked up in the coil as an oscillating EMF generated by the magnetic moments rotating back to equilibrium. The signal cannot be recorded directly, because its frequency is too high. It is mixed with a lower frequency signal to produce an interferogram of low frequency. This interferogram is digitized, and is called the Free Induction Decay, (FID). Fourier transformation of the FID yields a frequency domain spectrum.

FID – Time Domain Signal -à Fourier Transform -à Spectrum – Frequency Domain
Chemical Shift and the NMR Spectrum
Sigma Electrons and Electronic Shielding
Electrons are negatively charged particles that surround nuclei within a molecule. We know that moving charged particles will generate a magnetic field. For example, a stream of moving electrons (electrical current) will generate a magnetic field around the conducting wire that will cause the needle of a compass to align itself with the lines of force generated by the magnetic field. Since electrons around nuclei in a molecule generate their own magnetic field, the lines of force (magnetic moment) generated by this magnetic field will run in the opposite direction as the lines of force generated by the external magnetic field Bo. In fact, the electron’s magnetic field runs anti-parallel to the external magnetic field. When this happens, the electron-generated magnetic moment will run in opposition to the magnetic moment of the external magnetic field. This has the effect of reducing the net magnetic moment affecting the proton. This requires that the external magnetic field be greater or higher in order to overcome this opposition so that an NMR signal may be generated. This electronic magnetic field effect will cause protons with different chemical environments to yield resonance frequencies perturbed from the frequency defined by the applied external field Bo.
The Larmor frequency can be re-written to include the electronic effect:
ωo = γ(Bo – S)
where S represents the change in magnet field caused by the opposing electron magnetic moment.
All electrons making up the sigma bonding around the nuclei will generate a magnetic field that will be anti-parallel to the external magnetic field’s lines of force. This causes the NMR signal generation to occur at a higher external magnetic field setting. The NMR signal is shifted upfield, and the protons are said to be electronically shielded. The word shielded is used because the electronic magnetic moment actively shields the proton from the external magnetic field such that the effect of the external field is not as great as it could be if the proton was “naked”.
The Inductive Effect and Electronic Deshielding
Sigma electrons always shield spinning nuclei like protons and cause the NMR signal to be at a lower than expected resonance frequency. However if these sigma electrons can be diverted or shifted away from the proton nucleus, then the electronic shield they generate will be partially stripped away. This occurs when highly electronegative atoms like halogen, sulfur, oxygen, or nitrogen atoms are near these sigma electrons. The highly electronegative atoms attract these sigma electrons toward themselves and away from the proton nucleus. This is called an inductive effect, and it has the effect of stripping away part of the electronic shielding. As expected this phenomenon is called deshielding. If proton nuclei are deshielded then the NMR signal is generated at a higher resonance frequency. The deshielding is said to shift the signals downfield. Nearby oxygen, nitrogen, or halogen atoms attached to the same carbon or adjacent to such carbon atoms will cause an NMR signal to be generated further downfield.
π-Electrons and NMR Signal Generation
π-electrons also generate magnetic fields just like the sigma-electrons, but unlike the sigma electrons which always shield spinning nuclei, π-electrons can both shield or deshield proton nuclei depending upon whether the magnetic lines of force (magnetic moments) generated by the π-electron’s are parallel (deshield) or anti-parallel (shield) to the applied magnetic field. In general, π-electrons deshield the protons that are attached to the sp2 hybridized carbons. Thus, olefins and aromatics resonate downfield from protons sigma bonded to sp3 hybridized carbons
Chemical Shift and the TMS Standard
We have now determined that chemically different protons have different electronic environments. Differences in the electronic environments cause the protons to experience slightly different applied magnetic fields owing to the shielding/deshielding effect of the induced electronic magnetic fields. Over the years NMR spectra have been obtained on every conceivable organic molecule in nature or synthesized in a lab. In order to standardize the NMR scale it is necessary so set a 0 reference point to which all protons can then be compared. The standard reference that was chosen is tetramethylsilane (TMS). This compound has four CH3 methyl groups single bonded to a silicon atom. All of the protons on the methyl groups are in the same electronic environment. Therefore only one NMR signal will be generated. Furthermore, the electronegativity of the carbon atoms is actually higher than the silicon atom to which they are bonded. This results in the sigma electrons being shifted toward the carbon atoms in the methyl groups and consequently, the protons will be heavily shielded causing the one signal to be generated at a very high magnetic field strength setting. It is that signal that all other NMR signals of a sample are referenced to. This association with the reference signal is called the chemical shift. This shift is measured in parts per million (ppm). NMR signals occurring near the TMS resonance are said to be in an upfield position while those shifted away by deshielding are said to be downfield (see figure below).
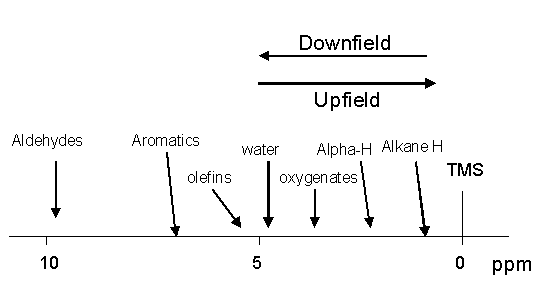
Virtually all NMR signals will be further downfield from the TMS signal because of the heavily shielded nature of the methyl protons in the TMS molecule. The proton NMR chemical shift range is 0-12 ppm. The ppm scale is another form of standardization that allows one to compare directly the 1H spectra obtained on NMR instruments with different magnetic fields. After the samples have been referenced to the TMS resonance at 0 ppm the actual NMR peak position in Hz is divided by the resonance frequency of the spectrometer, which is in MHz. Thus, one is dividing Hz by MHz which is a part per million (ppm). One ppm on a 58 MHz NMR instrument is actually 58 Hz from the resonance position of TMS, while on a 300 MHz NMR instrument 1 ppm is 300 Hz from the TMS resonance position. With this standardization/normalization in place one can always unequivocally say that all benzene protons resonate at 7.16 ppm no matter what NMR instrument is being used in the analysis.
In the Foxboro process NMR instrument we do not have an internal TMS standard available to reference the on-line spectra. Instead, the NMR peaks in the spectrum itself are used to reference the whole spectrum based on a well-established knowledge of the process stream chemistry. The various aromatic, CH3 or CH2 groups in the spectrum can be peak-picked and assigned to their known chemical shift values that have been logged in large databases of NMR chemical shifts. Below is a diagram showing the chemical shifts of some typical organic functional groups. The detailed chemical shift information related specifically to petroleum chemistry is described more fully later on.
Proton NMR Chemical Shifts for
Common Functional Groups
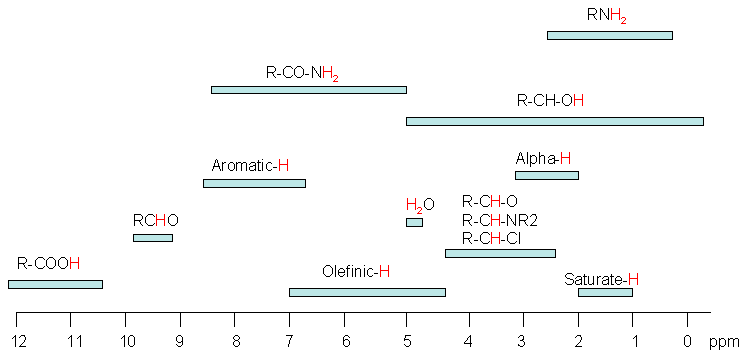
- Electronegative groups are “deshielding” and tend to move NMR signals from neighboring protons further “downfield” (to higher ppm values).
- Protons on oxygen or nitrogen have highly variable chemical shifts, which are sensitive to concentration, solvent, temperature, etc.
- The -system of alkenes, aromatic compounds and carbonyls strongly deshield attached protons and move them “downfield” to higher ppm values.
Relaxation
In most spectroscopic techniques, how the energy absorbed by the sample is released is not a primary concern. In NMR, where the energy goes, and particularly how fast it “gets there” are of prime importance. The NMR process is an absorption process. Nuclei in the excited state must also be able to “relax” and return to the ground state. The timescale for this relaxation is crucial to the NMR experiment. For example, relaxation of electrons to the ground state in uv-visible spectroscopy is a very fast process, on the order of pico-seconds. In NMR, the excited state of the nucleus can persist for minutes. Because the transition energy between spin levels (discussed earlier) is so small, attaining equilibrium occurs on a much longer timescale. The timescale for relaxation will dictate the how the NMR experiment is executed and consequently, how successful the experiment is.
There are two processes that achieve this relaxation in NMR experiments: longitudinal (spin-lattice) relaxation and transverse (spin-spin) relaxation.
In longitudinal relaxation energy is transferred to the molecular framework, the lattice, and is lost as vibrational or translational energy. The half-life for this process is called the spin-lattice relaxation time (T1). Dissipating the energy of NMR transitions (which are tiny compared to the thermal energy of the sample) into the sample should not be a problem, however T1 values are often long. The problem arises not in where to “send” the excess energy, but the pathway along which the energy is released to the lattice. Contributing factors to this type of relaxation are temperature, solution viscosity, structure, and molecular size.
In transverse relaxation energy is transferred to a neighboring nucleus. The half-life for this process is called the spin-spin relaxation time (T2). This process exchanges the spin of nucleus A with the spin of nucleus B (A mI = -½ ® +½ as B mI = +½ ® -½. There is no net change in spin for this process. Inhomogeneity of the magnetic field or the presence of paramagnetic materials can be a large contributor to the value observed for transverse relaxation.
The peak widths in an NMR spectrum are inversely proportional to the lifetime (due to the Heisenberg uncertainty principle) and depend on both T1 and T2. For most organic solutions, T1 and T2 are long enough to result in spectra with sharp lines. However, if magnetic field homogeneity is poor or paramagnetic material (such as iron) is present the NMR signals can be broadened to the extent that the signal is destroyed or unusable.
Processing the Free Induction Decay
We now have a signal corresponding to our NMR spectrum which contains a set of sine/cosine waves measured as a function of time and decaying towards zero intensity at an exponential rate (or more accurately to an intensity indistinguishable from the electronic noise in the receiver). This signal is said to be analogue, i.e. it varies continuously with time and is described as a time domain signal. There is little point in recording this on a chart recorder, since its complexity would make it unintelligible. Instead, it will be stored on computer memory, and to achieve this it needs to be digitized. This is done by sampling the intensity of the signal at discreet time intervals using a device known as an ADC (Analogue-to-Digital-Converter) and storing the intensity as an integer value ranging from 0 to e.g. 224 .
Two questions must now be answered; how frequently does one sample the FID, and for how long? The answer lies in the Nyquist Theorem, which states that to define a full (2p) cycle of a sine wave, its intensity must be sampled at least twice during one cycle. We need to sample at intervals which will therefore allow the highest frequency sine wave to be sampled, which in the example set out above is actually 600 Hz. Sampling must therefore occur every 1/2*600 = 0.0008333 seconds. To avoid losing information, our digital spectrum must eventually be able to distinguish between two peaks in the NMR spectrum say 0.293 Hz apart, similar in magnitude to the smallest couplings normally seen in standard samples, and referred to as the required digital resolution of the spectrum. This actually needs 2048 digital points in a spectrum that will be eventually 600 Hz wide (600/2048 = 0.293). Why did we pick exactly 0.293 Hz and hence require exactly 2048 points? Because all this digital information is going to be processed using a mathematical technique known as Fourier Transformation (FT), and FT’s are particularly fast (i.e. they are FFT’s) when the number of points processed is exactly 2n :
F(w) = º f(t) e-iwtdt
Here, the FID = f(t), and F(w) is the same data expressed as frequencies (=1/T) rather than as times and is called a frequency domain spectrum. This is the form we know for “conventional” NMR spectra, i.e. frequencies relative to an internal standard such as TMS. Equation (5) cannot be integrated analytically, and numerical methods such as the Cooley-Tukey algorithm have to be applied. The right hand side of the above equation can also be expressed as:
F(w) = ºf(t) cos -wt + º f(t)i sin -wt
which means that F(w) has two components, referred to as the real and imaginary parts. Each component contains the same frequency data but with a different combination of phase and amplitude. Only the real component is normally displayed. For 2*2n points in f(t), only 2n unique frequencies in F(w) are obtained. The total number of points to be measured to achieve an eventual resolution of 0.293Hz, over a width of 600 Hz, actually corresponds to 2 * 600/0.293 = 4096 points, and our total sampling time is 4096 * 0.0008333 = 3.41 seconds. At the end of this time, the time constants defining the exponential decay of q means it is normally close to zero, f(t) is effectively zero and the entire cycle can start again with a new pulse. Finally, we note that the time constants involved in the exponential decay of q (T1 and T2) are manifested in the Fourier Transformed function F(w) via 1/T, which has the same unit (Hz) used to measure the width of an NMR peak. Put another way, if M did not decay at all, T1 = T2 = ƒ and F(w) would have infinitely narrow and hence lead to unobservable lines, i.e. 1/ƒ = 0 Hz. This also explains why it is not a good idea to clean NMR tubes with chromic acid. Traces of this (paramagnetic) substance provide an excellent mechanism for M to relax, T1 ~ 0, and hence the peaks are infinitely wide, i.e. also unobservable.
Experimental Considerations
Temperature, Tuning, Locking, Shimming
The sample for an NMR experiment should not contain any particulate matter that may affect the field homogeneity within the sample. After the sample is stopped in the magnet it is necessary to tune the probe to get the most effective power transferred to the sample, and the most effective detection of the signal. Tuning the probe involves altering the complex impedance of the coil to minimize the reflected power. (This needs to be performed once during installation).
After the probe is tuned it is necessary to “lock” the spectrometer on the external LiCl sample.
Adjusting the Transmitter
The next step is set the frequency of the pulses and to adjust the sweep (or spectral width). In general, spectrometer frequencies are specified using two parameters, a fixed number that depends on the magnetic field strength of the instrument and the observed nuclei, and a user adjustable offset that is added to the fixed number to give the frequency of the transmitted pulse. At the beginning the user defined offset is set to zero and a very large spectral width is used (e.g. 20 KHz). With such a wide window all of the resonance lines should fall in this frequency range. Since the time required for the 90o pulse is not yet known, the first spectrum is obtained using a short (6 μs) pulse. Once the position of the resonance peaks has been determined, the offset is moved to the middle of the spectrum and the spectral width is adjusted to be just large enough to span all of the resonance lines in the spectrum.
The 90o pulse length is determined by observing the effect of the pulse length on the spectral intensity or on the FID signal intensity (RMS – root mean signal). The spectrometer frequency is set to be 300-500 Hz from the resonance frequency of the main resonances in the spectrum. The pulse length is set to 4 μs (e.g. << 90o) and a spectrum is obtained. The spectrum is phased to produce a positive absorption line. The pulse length is increased until the line goes through a maximum value of RMS or signal intensity (90o) and then reaches zero (180o). The pulse length is then doubled to produce a 360o pulse. The pulse length is slightly modified to produce a null signal. Final adjustment of the pulse length using 360o pulses avoids the necessity of waiting for the spins to relax.
Shim System
The shim system consists of a number of small coils that surround the area of the sample, which is contained within the most homogeneous region of the magnet. The purpose of the shim coils is to provide a means to make slight adjustments to the static magnetic field to increase its homogeneity. There can be a large number of coils, each of which generates a small magnetic field, which is shaped like a spherical harmonic. Since these functions are orthogonal the field generated by each shim coil is, in theory, independent of the fields generated by the other shim coils. However, in practice there can be considerable interaction and it is usually necessary to adjust several coils at the same time. All magnets show drift, or a change in field strength, over time. These changes are usually small enough that they can be compensated by adjusting the 1H transmitter frequency to match the magnetic field / shim changes.
The Lock
Changes in the magnetic field strength are detected by measuring the resonance position of Li7 in the external lock reference. Both the absorptive and dispersive components of the Li7 resonance line are used in adjusting for field inhomogeneity. Based on the absolute frequency of the Li7 resonance the transmitter frequency is adjusted to compensate for changes in magnet, sample, or shim.
Generating the Pulse
The actual frequency of the RF pulse is generated by mixing two frequencies together. The first, wsyn is adjustable and is generated from the frequency synthesizer under computer control. The second is an internal constant frequency called the intermediate frequency, IF. After mixing of these two frequencies and amplification the signal is sent to the probe. Since the same sample coil is used to both send the RF pulse and receive the FID it is necessary to route the RF pulse to the coil and not to the pre-amplifier. Otherwise the rather intense RF power may damage sensitive components in the pre-amplifier. This routing is accomplished by grounding the circuit (using diodes) 1/4l from the junction point. Under these conditions the pre-amplifier side of the circuit appears as an infinite resistance and most of the RF pulse goes to the sample coil.
Receiving
The induced transverse magnetization is detected using the same coil that carried the RF pulse to the sample. However, since the induced EMF in the coil is quite weak, the grounded point in the pre-amplifier is not seen as a ground and the signal can pass the 1/4l coil.
The frequency of the induced RF is quite high (e.g. 58 MHz). This is an extremely fast rate (i.e. 58 MHz) and there are practical problems associated with operating analog to digital converters at this frequency. Instead of trying to sample the magnetization at 58 MHz the frequency of the signal is reduced to that in the rotating frame (audio range) by mixing the signal first with wsyn and then with the IF.
Since the detected signal is the same as that calculated in the rotating frame we could use the same expressions as derived earlier:
Mx(t) = cos(wt)e-t/T2
My(t) = sin(wt)e-t/T2
If we only collect the signal from the x-axis then the resultant Fourier transform will produce two peaks, at +/- w. This would be quite problematic as the resonance peaks would be folded or mirrored about the reference frequency. To solve this problem, both components of the magnetization, Mx and My, can be detected (quadrature detection). However the probe only contains one coil. Therefore, we must extract the orthogonal signals from one FID.
This is accomplished by splitting the signal before mixing with the IF. Two IF mixers are used, one of which is at zero phase, while the other is shifted by 90o. The former produces a signal that is cosine modulated, while the latter is sine modulated.
Quadrature detection (see below) allows the placement of the spectrometer frequency in the middle of the spectrum. There are two advantageous to placing the spectrometer frequency in the middle of the spectrum. First, we require half as much transmitter power to cover the spectral width. This reduces resonance-offset effects. Second, less noise is folded into the spectra, thus increasing the signal to noise.
Digitization of the FID
Effects of the Discrete Fourier Transform
The signal produced by the orthogonal mixers is still in analog form. It enters analog-to-digital converters that produce a digital form of the signal. In is necessary to sample the analog signal at discrete points during the FID. The fastest rate of digitization that could be used is limited by how fast the analog to digital converter works. This rate of digitization is seldom used (except in NMR of solids) and much slower rates are quite acceptable for high-resolution work in liquids.
When setting up the digitization of the FID it is necessary to determine how long the FID should be sampled and at what rate (e.g. number of analog to digital conversions/sec). The practical limit on the length of acquisition time is dependent on the spin-spin relaxation rate (T2). There is little point in obtaining data for longer than 3-5 times T2 because the noise is of the same order of the signal. For modestly sized proteins the T2 is on the order of 50 msec; thus the total acquisition times should not exceed 200-300msec. The maximum resolution that is obtainable in an NMR spectrum depends on the inverse of the signal collection time. To obtain 1 Hz resolution it is necessary to digitize for 1 sec.
The second consideration is how often to sample the FID, or how long to wait before taking the next point (dwell time, t). The acquired FID can be considered to be a product of a continuous FID with a comb function. The Fourier transform of the FID is simply the spectra. The Fourier transform of a comb function in the time domain is another comb function in frequency space, spaced 1/t apart. The convolution of these two functions is a series of spectra spaced 1/t apart. If 1/t turns out to less than the frequency range of the spectral lines then each spectra will overlap with its neighbor, or the spectra will be aliased.
The origin of aliasing can be seen by considering the phase angle generated by the precessing spins. After a 90o pulse all of the different spins will be aligned along the y-axis. These spins will precess in the rotating frame with an angular velocity of wo-w, or at the frequency difference between the resonant frequency of the spin and the transmitter frequency. If a spin has a sufficiently fast angular velocity it can precess an angle of θ during the period of one dwell time. If this occurs then it is impossible to determine the path of the precessing spin, it could arrive at that position either by precessing in the positive direction an angle +θ, or in the negative direction by an angle -θ. To avoid this indeterminacy it is necessary to restrict the rotation angle during one dwell time.
Pulse Repetition Rate
Some time after the first FID is collected and digitized, another scan will be collected and added to the first. This will be repeated until a satisfactory level of signal to noise is obtained. Consider the effect of T1 on the relaxation delay (RD) time. It is important to pulse at a slow enough rate such that most of the magnetization is equilibrated along the z-axis such that the second (or third etc) 90o pulse generates an FID of similar magnitude. If the pulse rate is too fast the sample becomes saturated. The solution is to either wait longer between pulses (increase the RD time) or use a flip angle less than 90o. Under steady state conditions the optimal flip angle is given by the Ernst equation:
Cos βopt = e-T/T1
The above equation gives the best signal averaging for a given T1 however the signal amplitude is reduced for reduced flip angles. For T=3*T1 the amplitude is 95% of that obtained for a single pulse. For T=T1 the amplitude is 70% of that obtained for a single pulse. However, you can pulse three times as fast giving a three-fold increase in total signal.
The signal-to-noise ratio of a spectrum increases as the square root of the number of scans. This is because the signal strength increases in a linear fashion with pulse number, while the strength of the noise increases as the root of the number of pulses. To double the signal-to-noise ratio you must take four times as many scans. This reduces the advantage of using fast rates with flip angles less than 90o.
The equation that describes the steady state amplitude as a function of T is:
A=Ao(1-e-T/T1)
Instrumentation Artifacts
Digitization Errors
The Fourier transformation of the FID is accomplished using an algorithm that is described by the following equation:
F(rΔω) = ![]() Cos (rΔωiΔt)Δt
Cos (rΔωiΔt)Δt
The above requires the data to be represented in a digital form. Most modern spectrometers have 16-bit analog-to-digital converters, making it possible to digitize data over a range of 0 to 65,536. The fact that the signal has to be represented as bits implies that it is not possible to represent the signal with complete accuracy because the signal is likely to fall between the values represented by any two bits. This error is minimized by having as many bits as possible in the analog-to-digital converter.
There are three significant errors that occur as a result of the A-D conversion. The first is the effect of misrepresenting the signal because of the resolution of the digitizer. This causes images of spectral lines at various harmonics of the difference between the position of the line and the carrier frequency. These signals can appear as spikes or may be seen as increased noise in the spectrum. The best way to avoid these signals is to use all of the bits of the digitizer to represent the signal (i.e. adjust the receiver gain accordingly) and place the strong solvent line at the carrier frequency.
The second error is an extreme example of the first and occurs when there is a mixture of strong and weak signals in the spectrum. If the contribution of the weak signals is less than one bit, the A-to-D conversion cannot accurately represent these lines, and the weak lines will be distorted and lost in the noise. Either the gain must be increased, or methods must be found to attenuate the strong solvent line.
The third error arises if the gain is set to a level such that the signal exceeds the dynamic range of the AD converter. If this occurs the FID is said to be “clipped”. The points that are clipped will contribute incorrect weights to the Fourier sum, thus distorting the spectrum.
Signal Distortion
Measurement of the FID by the spectrometer can introduce artifacts beyond those discussed above. One such artifact occurs when the first few points of the FID are distorted by transient effects after the pulse (such as acoustic ringing). These distortions contribute to low frequency signals that distort the baseline. This artifact can be removed after the data has been acquired be either linear prediction (discussed later in the course) or shifting the FID to the left to remove the distorted points. The latter solution will necessitate a 1st order phase correction to the spectrum of 180o for each point removed.
Quadrature Imbalance
Imbalance of the real and imaginary channel can also cause artifacts in the spectrum. Ideally, the direct current (DC) offset of each channel should be zero and the amplification of each channel should be the same. DC offsets cause the appearance of a signal at zero frequency in the spectra (why?). Large DC offsets should be removed by proper adjustment of the instrument. Otherwise it is possible to overflow the AD converter with the offset. Small DC offsets can be removed before processing by adjusting the end of the FID to zero.
Channel imbalance results in the generation of quadrature images. The Fourier transform of properly balanced channels gives a single resonance line:
Cos(ωt) + i Sin(ωt) = eiωt → δ(ω)
However, if the channels show an imbalance of a factor ƒ, the detected signal is:
S(t) = (1+ƒ)cos(ωt) + i sin(ωt) → ƒcos(ωt) + eiωt
After Fourier transformation the second term gives the normal resonance line while the first term gives rise to a ghost image of the peak at ±w. Note that these ghost peaks are folded about the origin. The intensity of the ghost peak is proportional to the degree of channel imbalance.
Simple Phase Cycling to Remove Artifacts – Quadrature Detection
The effects of DC offset and channel imbalance can be corrected by simple phase cycling. For example, consider the effect of shifting the phase of the excitation pulse by p. To get the same signal from the receiver it will be necessary to shift the phase of the receiver by p as well. However, instead of shifting the phase of the receiver the routing of the data to computer memory is changed and a shift corresponds to subtracting the signal from memory. The effects of phase shifts of the excitation pulse on the signals coming from the detector and the receiver phase required to co-add the signals are shown below.
| Pulse phase | 0(X) | 90(Y) | 180(-X) | 270(-Y) | |
| Channel | X | sin | cos | -sin | -cos |
| (signal) | Y | -cos | sin | cos | -sin |
| Memory | R Data (cos mod.) | -Y | +X | +Y | -X |
| I Data (sin mod.) | +X | +Y | -X | -Y |
The DC offset will be canceled by the addition of two scans (with the appropriate receiver phase), one with a phase of 0o and one with a phase of π. This is because the DC offset remains the same, but the signal is inverted. The addition of the two spectra (actually subtraction) removes the DC offset. A π/2 phase shift will remove a quadrature image since it effectively switches which channel a given signal passed through. When they are added together in the computer any difference in the gain between the two channels is averaged out. These two phase cycles (0,π) and (0,π/2) can be combined to give a four step phase cycle:
| Pulse Phase | 0 | 90 | 180 | 270 |
| Receiver Phase | 0 | 90 | 180 | 270 |
This phase cycle is called CYCLOPS and is very efficient at removing artifacts associated with an imbalance in the DC offset and the gain of the two channels.
Note that the above method of changing the receiver phase has actually nothing to do with the phase of the signals going into the mixer. Rather it involves how signals are routed from the mixer and the ADC to the computer memory. Using this scheme it is only possible to generate receiver phase shifts of p/2. If receiver phase angle changes of less than p/2 are desired (these are seldom used) it is necessary to change the phase of the IF going into the mixer. This is usually done in the pulse sequence software by adding a small angle phase shift to the receiver. This phase shift is then added to the standard p/2 phase shifts and the desired phase shift is obtained by combining the phase shifting of the IF with changing the routing of the signals.
Truncation Errors
Truncation errors occur when the FID does not go to zero by the end of data collection. This is seldom a problem in one-dimensional spectra, is often a problem in two-dimensional spectra, and is always a problem in three-dimensional spectra. A truncated signal can be described as the product of a normal FID and a square wave. Therefore, the resultant spectra will be the convolution of the normal spectral line and a sinc-function. Truncated FID’s, and the resultant transformed spectra are shown below:
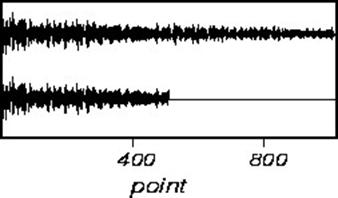
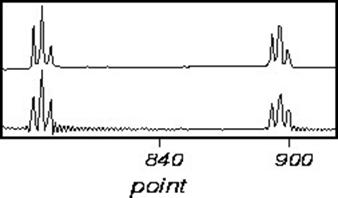
The effects of truncation can be removed by insuring that the FID is zero at the end of the data acquisition. This can be accomplished by either digital processing of the FID, or linear prediction. However, the easiest way to avoid this problem is to leave the receiver on for long enough to capture the whole FID included a small amount of noise to ensure the sinc-function ripple does not appear.
Digital Processing (Window Functions, Apodization)
The most common modification to the FID is exponential multiplication (EM) or line broadening (LB). The effects of window functions on the spectral lines can be seen by calculating transforms of the modified FID. For the LB, or EM, function we multiply the FID by e-t/a to give the following FID:
F(t)= e-t/T2e-t/a
F(t)=e-t[1/T2 + 1/a]
Without going through the math it is obvious that this transform will give a Lorentzian line, but with a modified T2:
1/T2’ = 1/T2 + 1/a
Usually the parameter 1/a (in Hz) is specified in LB routines. The optimal value of LB= Dƒ1/2 (the width of the lines in the spectra). The EM window function serves two purposes. First, it can force the FID to zero at the end of the acquisition time. Second, exponential multiplication reduces the noise in the spectra. If the FID decays well before the end of the acquisition time then there will be no loss in reducing the contribution of the noise in the tail end of the FID by damping it to zero. The appearance in the spectra is to reduce the high frequency noise at the expense of broadening the lines.
There are a number of other window functions commonly used in NMR. However, all of these distort the exponential decay of the FID and change the amplitude of the first point of the FID. The former produces non-Lorentzian lines, while the latter will affect signal intensity.
Trigonometric Windows: This group of window functions are members of a class of window functions designed to produce resolution enhancement. They are either sine or cosine functions with a period twice the length of the FID. These trigonometric functions are also squared to produce sine-squared window functions. The adjustable parameter in these window functions is the phase shift. A common window function would be a sine-squared function shifted 80o. This approximates a Gaussian to Lorentz transform. It has the desirable properties of bring the FID to zero at the end of the acquisition time. It enhances the higher frequency terms of the FID, hence resulting in resolution enhancement at the expense of increased noise and distorted lineshapes.
Increasing Spectral Resolution (Zero-Filling)
Linear prediction can be used to marginally increase spectral resolution by generating additional points beyond the acquired points. Additional spectral resolution can be obtained by zero filling. Zero filling is simply extending the FID with zeros. For example, the FID may decay in one-half of the time required to obtain the desired resolution. Thus there is little point in wasting computer memory collecting the latter half of the FID. However, a higher resolution may be desired in the final spectrum. This can be accomplished by doubling the size of the FID and setting the new values to zero. The subsequent transform will produce a spectrum with the desired resolution. This trick cannot be played indefinitely. Further zero-fills contain no further information and only serve to interpolate between the existing points.
The increased resolution that is obtained arises from the fact that the time evolution of the system is well defined. It is possible to regard the FID as extending in both positive and negative directions, thus providing twice the spectral resolution.
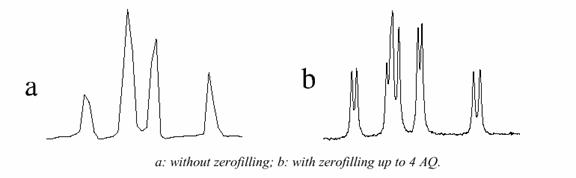
How to Obtain Quantitative NMR Spectra
The quantitative information of NMR is contained in the area under the various resonances. A quantitative spectrum is simply a spectrum where you can trust the integral values and ratios. In other words, if the integral of resonance A is twice the height of the integral of resonance B, you can say with certainty that resonance A is due to twice the number of nuclei as resonance B. In the Foxboro NMR instrument all spectra are converted to integral values during the data processing step. We use integrals because it is the area of the resonances that is proportional to the number nuclei. The height of a broad line may be less than that of a sharp line, but its area may be greater. How do we get accurate integrals? By ensuring that all resonances are equally excited, well digitized, and properly relaxed.
-
- Equally excited : if the pulse power is not high enough, some resonances far from the observe frequency may experience a reduced flip angle, resulting in a smaller observed signal. Fix: ensure power levels are high and that the spectrum is not offset to the edges of the spectrum.
- Well digitized : if the number of data points in the spectrum is too low, there will not be enough points to accurately define each resonance, resulting in inaccurate integrals (and peak heights). Fix: set ADC so that a narrow spectral width is defined and the FID contains all signal and very little noise – then zero fill to 8192 of 16384 points so that the spectral resolution is improved for referencing and integral calculation.
- Properly relaxed : resonances that are not fully relaxed give a weaker signal than fully relaxed resonances. The nuclei in your compound will not all relax at the same rate, so if you pulse too rapidly the quickly relaxing resonances will appear stronger than the slowly relaxing ones. To be sure of obtaining accurate integrals, one must ensure that a 45o pulse is used and that a relaxation delay is placed in the pulse sequence that is long enough to prevent observable RMS reduction from the first pulse to the second pulse. For small molecules in the gasoline range typical T1 values are on the order of 8-30 seconds while larger molecules in the diesel range are typically 4-20 seconds. The T1 of the longest relaxing molecule in the mixture must be used. Thus, at 45o the recycle rate should be about 10 s for gasoline range samples and 7 seconds for diesel range samples.
Proton NMR of Refinery Streams
Table I shows the chemical shifts of the various functional groups found in petroleum products.
Table I
Proton NMR Assignments for Functional Groups of Interest in petroleum Chemistry
Peak
Position * Assignment (comments)
0.5-1.0 CH3 g and further, some naphthenic CH and CH2 . Separation at 1.0 ppm is generally not baseline resolved (ref a).
1.0-1.7 CH2 b and further. some b CH. Separation at 1.7 ppm is generally not base resolved
1.7-1.9 Most CH, CH2, b hydroaromatic. This shoulder is one of the best available ways to estimate hydroaromaticity (ref b).
1.9-2.1 a to olefinic. Only if a clear peak appears, associated with peaks at 4.5-6.0 ppm
2.1-2.4 CH3 a to aromatic carbons. Separation at 2.4 ppm is generally not base resolved
- CH, CH2 a to aromatic carbons
- CH2 bridge (diphenylmethane)
- Olefinic
- Single ring aromatic
7.2-8.3 Diaromatic and most of tri- and tetraromatic. For differentiation of aromatic ring multiplicity see Cookson and Smith(ref a) and Simmons (ref c).
- Some tri- and tetraromatic rings
- Some tetraromatic rings
* Referenced to TMS (tetramethylsilane) at 0 ppm (units = ppm)
ref a Cookson, D.J., Smith, B.E., in ‘Coal Science and Chemistry’ (Ed. A. Volborth), Elsevier, Amsterdam,1987, pp31-60.
ref b Galya, L.G., Rudnick, L.R., Am. Chem. Soc. Div. Pet. Chem. Prepr., 1988, 33, 382.
ref c Simmons, W.W. (Ed.),’The Sadtler Handbook of Proton NMR Spectra’, Sadtler Research, Inc., Philadelphia, PA, 1978.
NMR Chemometric Modeling
Introduction
Chemometrics is the statistical processing of analytical chemistry data with various numerical techniques in order to extract information. The technique utilized for the Foxboro NMR product is partial least squares analysis which reduces the large amount of spectral data obtained on a process stream and reduces the information into principal components (factors) that describe the spectrum/measured parameter correlation in a data reduced manner
Chemometric Modeling of Refinery Streams
The data processing routines that are commonly used with near-infrared spectroscopy in analysis of refinery streams are being used to process the spectral data from the Foxboro NMR instrument. A series of mathematical manipulations of the data are used with a previously developed calibration model to predict the fuel content value of the property of interest.
RAW DATA, X à Chemometrics: f(X) à MON, RON, Benzene, T90, Cetane etc.,
Mathematical Tools
Chemometric data analysis routines consist of proven mathematical tools from the statistics and engineering literature. Tools range from baseline correction and smoothing to multivariate analysis techniques such as partial least squares regression, PLS, principal components regression, PCR, and neural networks. The detection of outliers and new and different samples will be handled by hierarchical cluster analysis followed by Mahalanobis distance testing of single-cluster subsets of the spectral data.
Why Use Chemometrics?
The complex relationship of fuel content to fuel property often requires a complex solution. Consider the property of research octane number, or RON. The RON value of a particular fuel depends in a complex way on the chemical composition of that fuel. Aromatics tend to increase RON, while long and very short saturated chains tend to decrease the RON value of a fuel. Each particular chemical species contributes uniquely to the overall RON value of a fuel. Some types of molecules strongly influence (negatively and positively) the RON number while others have a more modest influence. Many fuel and distillate properties are a weighted function of the array of fuel constituents. Chemometric techniques provide a means for extracting complex property information from subtle variations in the fuel spectrum that arise from variations in the array of chemical constituents present in the fuel sample.
Long Term Modeling Approach
The ultimate goal in process modeling with chemometrics is to develop the “global” multivariate calibration model. The global calibration model would be invariant through time on one instrument and across different instruments. Little progress has been made on the development of global models on near IR instruments over the past 10 years. The global model would require that the calibration developed on one instrument be transferred to other instruments and through time on a single instrument without a significant loss of accuracy. This is a very challenging problem because of the complexity of the model being transported.
Process NMR Associates recognizes that chemometric process models must be developed and maintained. The strategy being implemented currently involves the updating of on-line models with new data points currently not described in the calibration models. This step is performed when a shift in the process is indicated by the appearance of outliers arising from chemical variation of the process stream. The expected maintenance interval for a given calibration is expected to decrease with time as the process variation is revealed and incorporated into the model database.
Chemometric Regression Methods
Model Building Using Soft Modeling Methods
Modeling in the absence of a direct quantitative physical understanding of the relation between the measurement variables(spectra) and the physical or chemical properties (e.g. RON) to be determined requires a different approach when compared with models based on well-defined physical systems. Take for example the property of Research Octane Number, RON. RON is known to depend on the distribution of chain lengths and fractional content of aliphatics, and on the distribution and fractional content of aromatic species. Even if the exact impact (hard model) of each molecular type on the octane number was quantitatively known, the accounting for the hundreds of chemical species that make up a gasoline stream would require an exhaustive level of analysis to compute the hard model for the fuel octane. Soft modeling with principal components makes use of the statistical correlation of the data variation with the property variation in developing a regression model.
Soft modeling was originally used in the behavioral sciences in an attempt to extract expected behaviors from complex multivariable observations. Modeling in the behavioral sciences is complicated by the selection of observations that are related to the behaviors of interest. Fortunately, the intuitive link between spectroscopic measurements and physical or chemical properties is much easier to establish. For example, it is known that 7-9 carbon straight chain aliphatics increase octane and that aromatics also increase octane. Aliphatics with a high degree of branching also increase the octane value of a fuel. Spectroscopy provides information on the chemical structure variation contained in the fuel mixture. Therefore chemical intuition can be used to support the development of regression models that relate the spectral responses to the octane number of fuels.
Multivariate Regression Models
Many engineers and scientists are familiar with the concept of linear regression. In linear regression a single independent variable, y, is regressed against a single dependent variable, x. The form of the regression model is:
y = bx + int (1)
Equation 1 requires 2 pairs of (x,y) data (2 points to define a line) since there are two unknowns to be solved, b and int. This theme of the number of data samples meeting or exceeding the number of unknowns to be determined is a very important concept that must be met in order to determine meaningful regression solutions. The solution to equation 1 is obtained by regressing known values of y against the corresponding known values of x. The unknown free parameters to be solved are the slope b, and the intercept, int.
In spectrometry, a line is used to develop a calibration between concentration, c, and absorbance, x, according to beer’s law.
c = bx + int (2)
It is possible to extend the regression relation to multiple concentration and absorbance variables. A vector is denoted by using a boldface lower case character, and a matrix is denoted by a boldface upper case character. The concentration vector includes the concentration of n sample constituents, a 1 by n dimensional vector.
c = xB + int (3)
Note that equation 3 has a 1 by n vector of concentrations(1 sample with n constituents), a 1 by m vector of spectral measurements, x, and an n by m matrix of regression coefficients(slopes) to be solved: (1 by m)(m by n) gives a 1 by n dimensional concentration vector.
If c and x are mean-centered, the intercept term is zero.
c = xB (4)
Equation 4 is the form of a multivariate predictive model that is used in the estimation of the property or concentration values of a sample with measured spectral response x. The predictive model is defined by B, the matrix of regression coefficients. A multivariate calibration model must be calculated to obtain B. In the calibration sequence, multiple samples are required to ensure a unique solution of B and the variables in the expression are all matrices.
C = XB (5)
The matrix of unknown free parameters, B, is solved by a multivariable matrix regression
B = (XTX) –1 XTC (6)
Where the superscript T is used to denote the matrix transpose, and the superscript –1 is used to denote the matrix inverse.
It is important to note that the matrix B, is dimensioned as m by n, the number of number of wavelengths, m, by the number of constituents, n. Equations 5-6 describe the multiple linear regression model, MLR. If it is desired to increase the available spectral information in the model, more spectral wavelengths are included. One of the problems with MLR is that the size of the B matrix of unknowns grows rapidly as more spectral wavelengths are included in the regression model. This means that the number of calibration samples with known property/concentration values must also grow rapidly as more wavelengths are included in the model. The failure to use an adequate number of calibration samples can result if a catastrophic failure of the model in the prediction mode. Another problem with MLR is that, for spectral data that exhibit subtle variations with the typical process variation, the matrix inverse step is poorly conditioned. A poorly conditioned system will lead to large errors in the computation of the regression coefficient matrix B, and resulting poor prediction accuracy. A poorly conditioned calibration matrix will lead to models that will be extremely unreliable in predicting on samples with spectra that are dissimilar to those spectra contained in the calibration set data. Dissimilar spectra are likely to be encountered with a changeover in blending feedstock or formulation (winter/summer) changes in the product.
Latent Variable Based Soft Models
The aforementioned difficulties with MLR are addressed with latent variable regression methods. A latent variable is defined as a variable that is not directly observable, but is related to the observable variable. The observable variables, usually spectral intensities or absorbances, are used to generate latent variables. A latent variable, t, is the result of a weighted linear combination of the observable variable vector elements, x.
t = p1x1 + p2x2 + p3x3 + p4x4 + p5x5 + … pmxm (7)
Thus, information from m wavelength measurements can be compressed into 1 latent variable. The weighting coefficients, pi , in equation 7 are called the loadings, and p is the loadings vector. In practice, more than one score variable is required to capture the relevant chemical variance of complex samples. The spectral matrix is eigen-decomposed into a number of scores and loadings vectors and some analysis is required to determine the number of that are needed to capture the chemical variation inherent in the chemical system. The number of relevant scores kept is typically between 5 and 10 when calibrating on petroleum distillate streams. Most of the methods of eigen-decomposing spectral data yield orthogonal or nearly orthogonal sets of scores. Orthogonalization of the spectral data addresses the problem of inverting a poorly conditioned spectral calibration matrix, and the relatively small number of score terms used can dramatically reduce the number of free parameters to be solved. This means that fewer samples are required to over-determine the calibration model. For example, the use of 500 wavelength measurements to determine 5 constituents would require 500*5 or 2500 unique sample spectra. If 10 scores were used in place of the raw spectra, 10*5 or 50 samples would represent the number of samples to exactly determine the chemical system. Experience has determined that reliable models should be over-determined by 2-3 times, therefore 100-150 samples (as opposed to 50) would be a good starting point to model a system with 10 significant scores.
Building of PLS/PCR Models
The two most common latent variable modeling methods are principal components regression, PCR, and partial least squares, PLS. They are essentially equivalent in modeling accuracy with the following exceptions:
- PLS may have an advantage in modeling systems that contain uncorrected baseline variation or pink noise.
- PCR may have an advantage in systems that contain more than 6 significant score variables.
The basic difference between the two is that the PLS algorithm uses information in the independent variable matrix of properties/concentrations to direct the decomposition of the spectral matrix into loadings vectors and scores while the PCR algorithm decomposes the spectral matrix sequentially in the direction of maximum spectral variance, subtracts the contribution on the maximal axis of variance from the spectral matrix, and then repeats the process along the maximum direction of variance in the residual spectral matrix that is orthogonal to the previously determined loadings vectors. This process is continued until the variance in the spectral matrix is completely eigen-decomposed.
The following discussion on process modeling specifics will focus on the use of PCR, though the choice of method actually used in process modeling will be determined by prediction accuracy.
Model Development Environment
Proprietary algorithms used in generation of calibration models, calibration transfer and spectrum pre-processing have and will be developed in the MATLAB programming environment. The PLS and PCR modeling program used to develop the process chemometric models is Galactic Grams PLS/IQ.
Principal Components Regression, PCR
Consider fuel spectra that are arranged in rows of a matrix of spectral data, X, with measured property values for each fuel sample represented in the property matrix Y. The development of the PCR calibration model is performed as follows:
First, the row spectral matrix X is decomposed into an orthogonal basis set of scores, T(projections), and loadings vectors contained in the matrix P as in Equation 1. The set of loadings vectors make up the basis for the new coordinate system. The new coordinate system is used to define the NMR spectrum in terms of new variables that are fewer in number than the frequency range variables that makes up the original NMR frequency coordinate system. The redefining of coordinates is analogous to the conversion from rectangular to polar coordinates, though coordinate changes in a PCR decomposition only require linear transformations. The values of the spectral intensities in the new coordinate system are the spectral scores, T.
X = TPT (8)
Selection of Principal Components
The number of coordinate (loadings) axes chosen to represent the spectral data (number of principal component scores) is a critical decision that will be made using a variety of criteria. The inclusion of too many scores leads to good fits of the model but sub-optimal prediction due to the inclusion of excess noise in the calibration model. The inclusion of too many scores leads to a model with excessive bias or systematic error in fitting and prediction. There are a number of methods (like PRESS, indicator function, f-test) that have been used to determine the optimal number of scores, but since some of these methods are statistically based and include statistical assumptions of data homogeneity, the most reliable method of determining the optimal number of scores is by expert inspection of the data structure. A careful study of the spectral calibration matrix is conducted and the residual errors fitted with the addition of each principal component are examined. Unusually large projections of a single sample on a single loadings axis can be indicative of one unusual sample dominating the score. In this case the score will be excluded from the model. In process modeling, the removal of one extra score component than the apparent optimal number, is often used to define models as it is easier to compensate for model bias than model noise.
Once the spectral scores of the calibration set spectra are obtained, they are then used along with the known matrix of property values to solve for the matrix of regression coefficients, B, which define the PCR calibration model.
B = (TTT) –1 TTY (9)
The calibration model is defined by the loadings matrix, P, and by the matrix of regression coefficients, B. Once the model is defined, the forward prediction step can be used in the evaluation of fuel properties as follows:
First, obtain the vector of scores, ti , for the ith fuel sample by projecting the sample onto the basis set or loadings matrix of the calibration model, P.
ti = xiP (10)
The prediction of the fuel properties, c, for the ith sample are obtained by right hand matrix multiplication of the scores vector by the matrix of regression coefficients as in Equation 4.
ci = tiB (11)
Sampling Requirements
There are well-defined statistically designed sampling guidelines for modeling with multivariable systems. A statistical design of the simplest type, a two-level design, requires two samples for a line (a univariate system: 1 independent variable), four for a plane (2 independent variables), eight for a cube (three variables) and so on. The formula for a statistical design of this type is 2n samples, where n is the number of variables in the system. Samples are strategically chosen in a high-low format in each variable with all combinations of high-low in each dimension accounted for. This design provides for interpolation of all samples that fall inside the (hyper)volume bounded by the calibration set measurements. Failure to use a statistical calibration design means that extrapolation of the calibration model along one of the loadings axes is likely to occur in the prediction mode.
Statistically designed calibrations models are not practical in many process applications because the extremes of the process are undesirable and therefore extreme samples are typically unavailable. This fact necessitates an alternate strategy for building process calibration models:
- An initial group of samples is selected containing as much of the process variation as possible. The model is built on these samples and the future prediction samples are evaluated in the prediction mode.
- If a prediction sample appears to represent a variation that is not present in the calibration set, the sample is captured, evaluated with the reference method (e.g. octane engine) and the model is rebuilt with the inclusion of that sample in the calibration set.
Approximately 50-75 fuel samples, each with lab determined property values, are needed to initially define a model containing 6-8 significant score components.
Model Adjustments
An adjustment of the model is dictated by the (automated flag) detection of process fuel spectra that are dissimilar to the existing fuel spectra in the model database. The differences could be due to considerable changes in chemical composition of fuels, malfunction of sampling hardware or spectrometer The detection of an unusual sample triggers a lab test, a graphical evaluation of the sample spectrum and, if necessary, a recalculation of the chemometric regression model including the new sample(s). These situations can arise from, process changes, unusual process disruptions/maintenance, changes in regulations concerning fuel content, or from absence of some (seasonal) variants of the fuel composition. In the case of regulation changes, some of the older fuels will be excluded from the model database so that the model reflects current blending targets. Model adjustments are commonly accepted among refiners that use spectrometry as a part of a unified process control strategy. It is felt, however, that model adjustments for NMR based models will be much fewer in number once a wide range of process conditions have been included in the model.
The “outlier” sample in question would be linked to a cluster in the calibration set and a Mahalanobis distance (a covariance matrix, C, scaled Euclidean distance) would be used to determine if the sample belongs to the identified cluster.
D = [(x-u)C–1 (x-u)T]1/2 (12)
The Mahalanobis distance of normally distributed spectral data is known to follow the c2 (chi-squared) distribution, permitting a test against a 95% confidence limit, assuming that the data are homogeneous and normally distributed. This test also assumes that enough data have been collected to obtain an accurate estimate of the sample population co-variance matrix, C. In the real world of refinery measurements, the data are clustered according to stream and the assumption of homogeneity fails. The normality of the data may also be in doubt, but the Mahalanobis distance is somewhat tolerant of modest deviations from normality.
To prevent the use of the Mahalanobis distance on a heterogeneous (multiple cluster) data set, the calibration set data will be partitioned into individual cluster groups and a class covariance matrix will be calculated for each cluster. This step will be performed using hierarchical clustering to establish the number of clusters, and then self-organizing clustering to assign cluster membership. The Mahalanobis distance of the sample will be calculated for each cluster and the sample will be evaluated with the c2 test statistic at the 95 % confidence level to determine is sample belongs to an existing cluster. If it is determined that the sample does not belong to an existing cluster and it is determined that there was no hardware malfunction, the model would be rebuilt with inclusion of the outlier sample in the calibration data set.
Process Spectrometers
Near Infrared, NIR
The most widely used process analyzers on the market use near-infrared technology. The strengths of near-infrared technology include:
- low sampling error
- high signal to noise ratio,
- multiplexed fiber optic sampling devices,
- relatively long maintenance intervals.
Among the weaknesses of NIR technology are:
- weak analytical signal variance of overtone and combination band vibrations
- heavily overlapped near IR spectral bands require the use of more complex mathematics to extract chemical and physical information
- baseline drift that may be as large as 50 times the thermal noise of the detector
- fiber optic sampling devices that can lead to shifting backgrounds
The heavily overlapped spectral bands that exist in the near-infrared region require sophisticated multivariate mathematics in order to take advantage of the high signal to noise ratio of the spectral measurement. Unfortunately, the reliability of multivariate process models is dependent on removal of the baseline drift in the spectra of the standard and the measurement samples as compared to the reference background, and in gradual changes in optical alignment or monochromonator mechanicals. Simple offsets or ramps in the baseline spectrum are easy to remove, while complex, nonlinear baselines due to variations in source output or detector phasing errors are more difficult to remove. Derivative methods are typically used to correct for baseline variations, though complex baselines are difficult to remove by derivative transformations, and high frequency noise is enhanced compared with the lower frequency signal components in the derivative transformation process. The failure to effectively remove these baselines or the enhancement of high frequency noise through derivative transformations can lead to a substantial loss in the ability to model NIR data accurately with multivariate regression techniques.
The complexity of the near-IR spectra for motor gas blending streams can lead to 6-10 significant principle components in a PLS or PCR calibration model. That is, the data contain 6-10 significant, mutually orthogonal coordinate axes. A simple two level experimental calibration design would contain 2n calibration samples of designed composition to prevent extrapolation of the regression model. Because refinery process streams do not generally contain samples of designed (extreme) composition, it will be necessary to extrapolate the calibration model in the prediction mode with the increased risk of large prediction errors. For these reasons, the detection of outliers is used to prevent large extrapolations of the regression model.
Nuclear Magnetic Resonance, NMR
High resolution Nuclear Magnetic Resonance spectroscopy is a relative newcomer to process chemistry though it is highly exploited in petroleum product research. Proton NMR, in particular, contains a great deal of information about the chemical composition of complex sample mixtures. Peak position is fundamentally related to the connectivity of the nuclei and splitting patterns (sometimes represented as broadness of features) contain information about the connectivity of neighboring nuclei. FT-NMR spectra obtained at small tip angles, are linear and additive in nature. Additivity, and the highly resolved nature of the NMR analytical spectra lead to better-conditioned and more reliable calibration models. NMR spectral differences of different diesel fuels are quite pronounced. Diesel fuels are obviously distinguishable by the ratio of CH2 to CH3 peak (directly related to average alkane/aromatic side chain length) and by the broadness of the aromatic features from 7-8 PPM (vs TMS). Narrow aromatic features are low in polynuclear aromatics while the broad aromatic signature is representative of fuels that contain significant percentages of polynuclear aromatics. Aromatics content and aliphatic/aromatic side chain length are directly related to the fuel cetane number and other properties. The chemical information is so well resolved in NMR spectra that early research into the cetane determination of fuels by NMR was performed without chemometrics (ratios of integrated frequency intervals were used) with analytical reproducibility’s of 1.3 cetane number. NMR is free of the baseline drift issues that plague near-IR. NMR instruments do not have moving parts that can fail mechanically, so the maintenance interval is expected to be even longer than that for near-IR. A permanently installed flow through probe means that mechanical positioning and alignment issues do not limit calibration accuracy through time. Finally, the NMR measurement is not susceptible to light scattering and other optical disturbances common in optical spectroscopy.
Another area of concern with NMR is in the maintenance of magnetic field homogeneity. Foxboro NMR has automated shimming routines and is currently testing a method for “on the fly” analysis of field homogeneity. Testing conducted to date indicates that field homogeneity may not be as important as might be suspected: integral areas remain the same under changing field homogeneity so the use of integrated spectral intervals of 0.1 to 0.5 PPM should deliver accurate models that are not significantly dependent on minor variations in the magnetic field homogeneity. The signal-to-noise ratio of NMR can be enhanced by averaging multiple measurements obtained from repeated pulsing and measurement, though the signal to noise is not likely to meet or exceed that of NIR. Finally, another opportunity for extracting even more information from the petroleum distillate samples may exist in the use of multiple pulse techniques.
NMR vs. NIR
NIR process instruments have been implemented in hundreds of refineries worldwide. The benefits of process NIR measurement include high signal to noise ratio, long pathlengths that provide good statistical samples, fiber optic multiplexing capability, maintenance intervals that are superior to the last generation of gas chromatographs, and moderate cost. NIR may have displaced gas chromatography as the process instrument of choice because of the maintenance down time advantage alone.
The strengths of NMR lie in the relation of the measurement signal to first principles and in the high resolution of the chemical information contained in the signals. NIR depends heavily on chemometrics techniques to extract information from the heavily overlapped spectral signals. Unlike NIR, the NMR spectra of protons attached to the key functional groups of aromatics, aliphatics, and olefins are mutually orthogonal to each other. Even polynuclear aromatics are easily distinguishable from single ring aromatics in the NMR frequency spectrum. These key facts should have a large impact on the accessibility of the chemical information that is required to characterize petroleum distillate streams. Also, the simplicity of a latent variable calibration model is not only due to the number of principle score components used in the model, but to the distribution of chemical information among the scores. Because specific NMR spectral information (like aromatic information) is more resolved than NIR spectral information, it will be distributed in a fewer number of component scores even if the overall number of scores used is the same. A dramatic improvement in the accessibility of the chemical information will lead to process models that are simpler, easier to maintain, and more robust when extrapolating in the prediction model or detecting outliers. NMR technology is initially more expensive than NIR, but the lack of moving parts should lead to maintenance intervals that are even greater than those for NIR.
Lastly, a new figure of merit should be defined for process chemistry. The typical signal variance to noise ratio will be more reliable in determining the precision and accuracy of property predictions. Consider a univariate measurement/calibration for simplicity: If the NIR signal is 0.4 Au and the noise is 0.001Au, but the signal variance is 0.01 Au for a range of 20 octane numbers, the signal to noise is 400:1 and the signal variance to noise (for 20 octane number range) is 10:1. A standard analytical calculation using signal to noise would suggest 1 part in 400 error in a typical octane value (89 gives about 0.3 octane numbers), but the actual signal variation would suggest a 1 part in 10 error over the 20 octane range or 2 octane numbers. For this reason, the signal to noise of NIR signals are misleading figures of merit that will not be useful in comparing with the NMR signal, that varies about 15 to 20 percent over a 20 octane range. Furthermore, the noise statistics generated by NIR spectrometer manufacturers do not include intermediate or long-term baseline drift through time! Direct comparisons of NIR and NMR on fuel analysis will reveal a more quantifiable expectation of spectrometer performance.
Copyright – Process NMR Associates LLC, 1998-2012